引言
众所周知，我们听到的声音是由于振动而产生的。声音的传播形式是波，那么它就会具有“频率（frequency）”这个属性。我们所听到的各种乐器，例如钢琴、小提琴，它们为何能演奏出相同的音高呢？这就要牵涉到音名与频率了。
这个话题的起源源于昨晚的一次群聊，我们在讨论各种钢琴音源，然后有人说：“mdaPiano！”然后我就附和说：“mdaPiano特别好听，简直是钢琴界的黑马。高音支持到B9999999，低音支持到A-12138！”说完，我突然想：“不对，这我要计算一下。”于是开始了计算大坑。计算过程我们留到后面再说，我们要先学习音名和频率的互换。
十二平均律
现行的国际标准音高为1939年5月国际标准协会在伦敦通过的A4=440Hz。下面所有的计算都以它为绝对标准。现在国际上用得最多的律制是十二平均律，它是由我国明朝音乐家朱载堉发明的。我们现在可以提取一些关键的信息：
一个八度被分为12个半音，一个半音被细分为100个音分。
半音和音分
那么我们就可以推得A5的频率是880Hz，同样地，A3的频率是220Hz。而A3-A4之间差距的220Hz是12个半音，那么我们就可以轻易推得A3-A4间的任意音名的频率了。
由于音名和频率之间并不是线性关系，当音高非常高时，半音间的频率差距也会非常巨大，所以我们必须要精确到音分级。前面已经说过一个半音被分成100个音分，那么一个八度就被分为1200个音分。但，差距的220Hz究竟是怎么得来的呢？那么这个时候，我们就要接触两个概念：半音比和音分比。
半音比
因为相邻半音（semitone）和音分之间的频率差距并不是简单的加减变化，设想若是简单的加减变化，而每个八度之间的频率差距并不相同，若是简单地平分，那么就会出现例如C5和C4的频率比不是2的问题。所以相邻半音和音分间的频率比一定相同。由于一个八度间的频率比是2（高比低），那么开十二次根号就是半音比了，也就是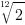
。计算可以得到
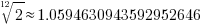。根据我们之前所知道的A4的频率是440Hz，我们便可以求得C4的频率。
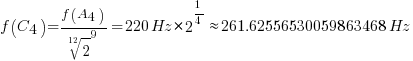
以此类推，我们还可以计算出#C4的频率，这里就有两种算法了：
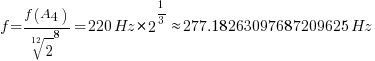
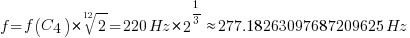
第一种方法是根据A4频率反推的，第二种是根据C4频率正推的。两种方法结果是一样的。
音分比
前面已经说过，把一个半音再分为100份便得到了音分（cent）。那么我们可以如法炮制地计算出音分比。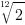再开100次根号便是
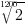。计算可以得到
。
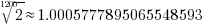例如我们要计算A4高18音分的频率，就要把A4的频率乘以音分比的18次方。
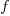
逆运算
在学习了半音和音分的基本计算之后，我们要学习一下基本逆运算。逆运算可以让我们根据频率推算音名。就如同指数运算与对数运算一样。例如我们已知频率为27.5Hz，求它对应的音名。根据之前的推导我们便可列出一个通用方程。
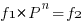
这里的P指的就是半音比或音分比。f1我们已知是440Hz，f2也已知是27.5Hz，那么我们要求的就是中间要变化的次数，也就是半音数或音分数，再根据一个八度包含12个半音或1200个音分就能推出对应的音名。
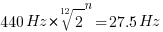
解上述方程可得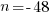
。也就是A4往下低48个半音就是27.5Hz，也就是低4个八度。那我们就求得了：27.5Hz对应的是A0。
